Introduction:
In February 1981, a historic achievement was made by several hundred international mathematicians over a period of thirty years which was completing the
classification of finite simple groups. The most interesting of the finite simple groups are the twenty-six sporadic groups. The sporadic groups acquired
their name as they do not belong to any infinite family of finite simple groups. The first family of these are the Mathieu groups which consist of
and ; which are permutation groups on and points, respectively, and they were discovered by
Emile Mathieu in 1861. The second family are the Conway groups which are , and , they may be considered as automorphism groups of the Leech lattice.
They were discovered by John Horton Conway around 1968. Despite the fact that before then the Higman-Sims group was discovered by D. G. Higman, C. C. Sims and
the McLaughlin group was discovered by J. McLaughlin, they are contained in both and . Meanwhile, the Suzuki group Suz was discovered by Suzuki
and the Hall-Janko group was discovered by Hall-Janko which may be considered as subgroups of the first Conway group. Although the rest of the twenty-six sporadic
groups are not discussed in this paper, we introduce them briefly. A century after finding Mathieu’s group, in 1966 Zvonimir Janko found the first Janko group
which has only elements. During the following decade a further twenty sporadic groups were discovered. In 1974, the largest group
of the sporadic groups, the Monster group or ( Fischer-Griess group) was discovered by Fischer. Moerover, in 1980, Griess constructed this group
as an automorphism group of dimensional algebra that has remarkable commutative but non-associative elements and the order of was computed by Thompson.
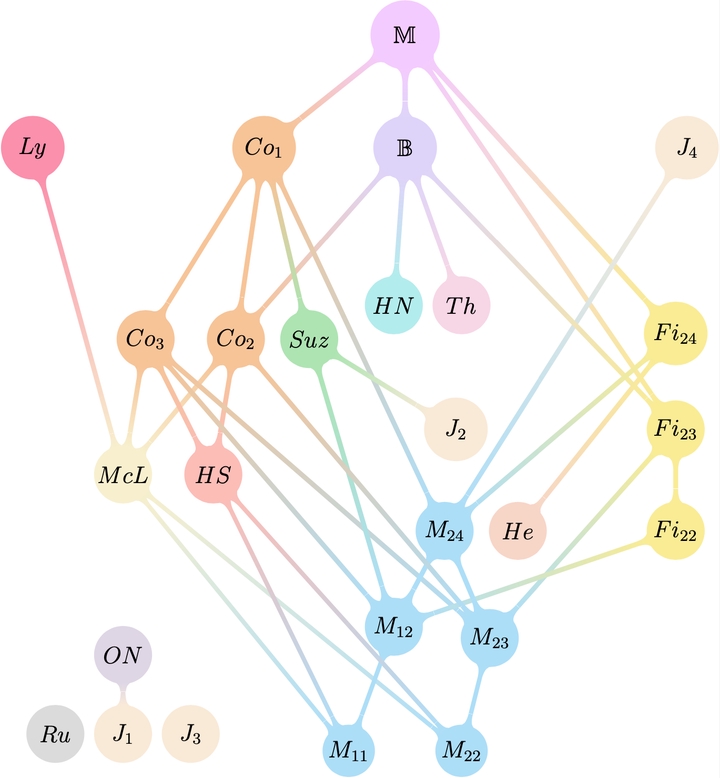 Genetic relation between sporadic finite simple groups
Genetic relation between sporadic finite simple groups